Many-Body Quantum Dynamics
My core research interest is the dynamics of many-body quantum systems, particularly far-from-equilibrium. These systems are notoriously difficult to study theoretically due to the exponential growth of the Hilbert space with system size, and the polynomial growth of entanglement entropy with time. This makes numerical simulations using classical computers extremely challenging. My research in this area focuses on developing new methods and algorithms to simulate these dynamics, as well as understanding the fundamental physics that governs them.
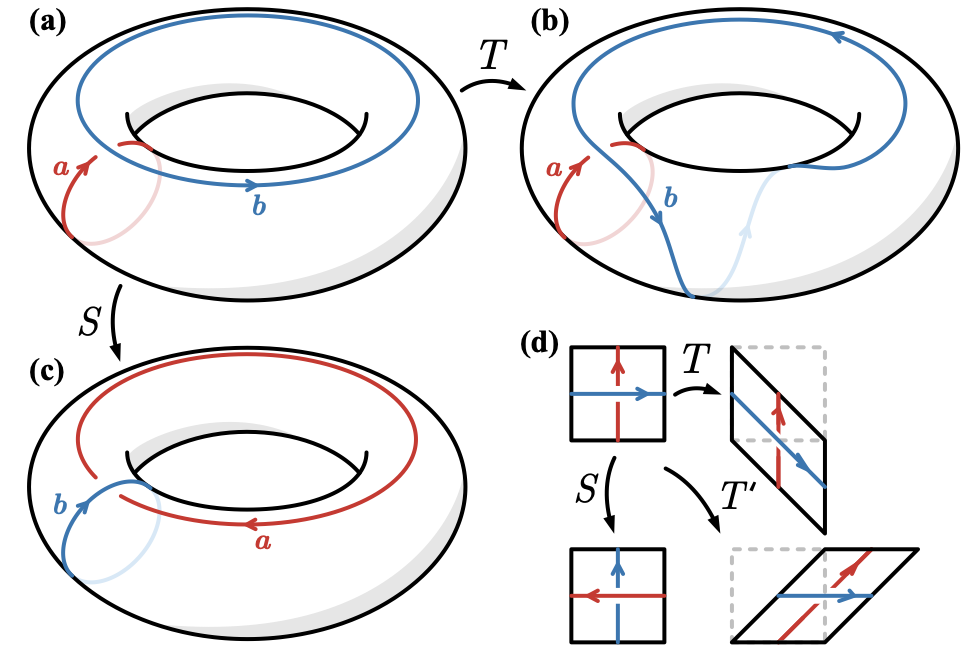
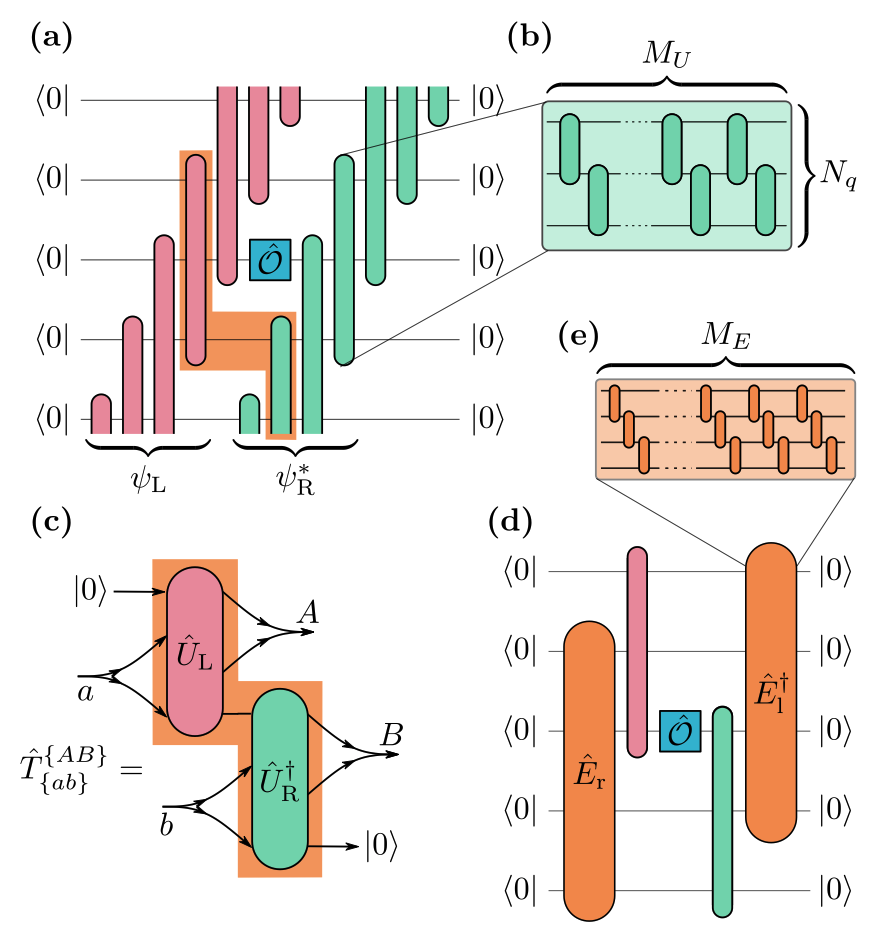
A natural language for describing many-body quantum systems is that of tensor networks. These provide an efficient representation of quantum states with limited entanglement, and have been successfully used to study ground states and many-body dynamics. They are also a natural framework for describing quantum circuits. I have been developing new quantum and classical algorithms for simulating many-body quantum dynamics using tensor network methods. I am increasingly interested in the entanglement and correlation structure of different classes of quantum circuits, as well as open quantum dynamics facilitated by measurement and feedback in quantum computers.
Quantum Computers
I am very interested in the use of quantum computers for simulating many-body quantum systems. These precisely controlled and isolated quantum devices are potentially ideal platforms for simulating quantum systems. Moreover, studying quantum many-body physics may be one of the few applications of quantum computers that can provide a genuine quantum advantage over classical computers before large-scale, fault-tolerant quantum computing is achieved. There is currently exciting and rapid progress in the development of quantum computers using a range of technologies. With that said, as of yet there has been no clear demonstration of this advantage. However, this effort has been providing a deeper understanding of quantum many-body systems as well as the classical and quantum algorithms that can be used to study them.
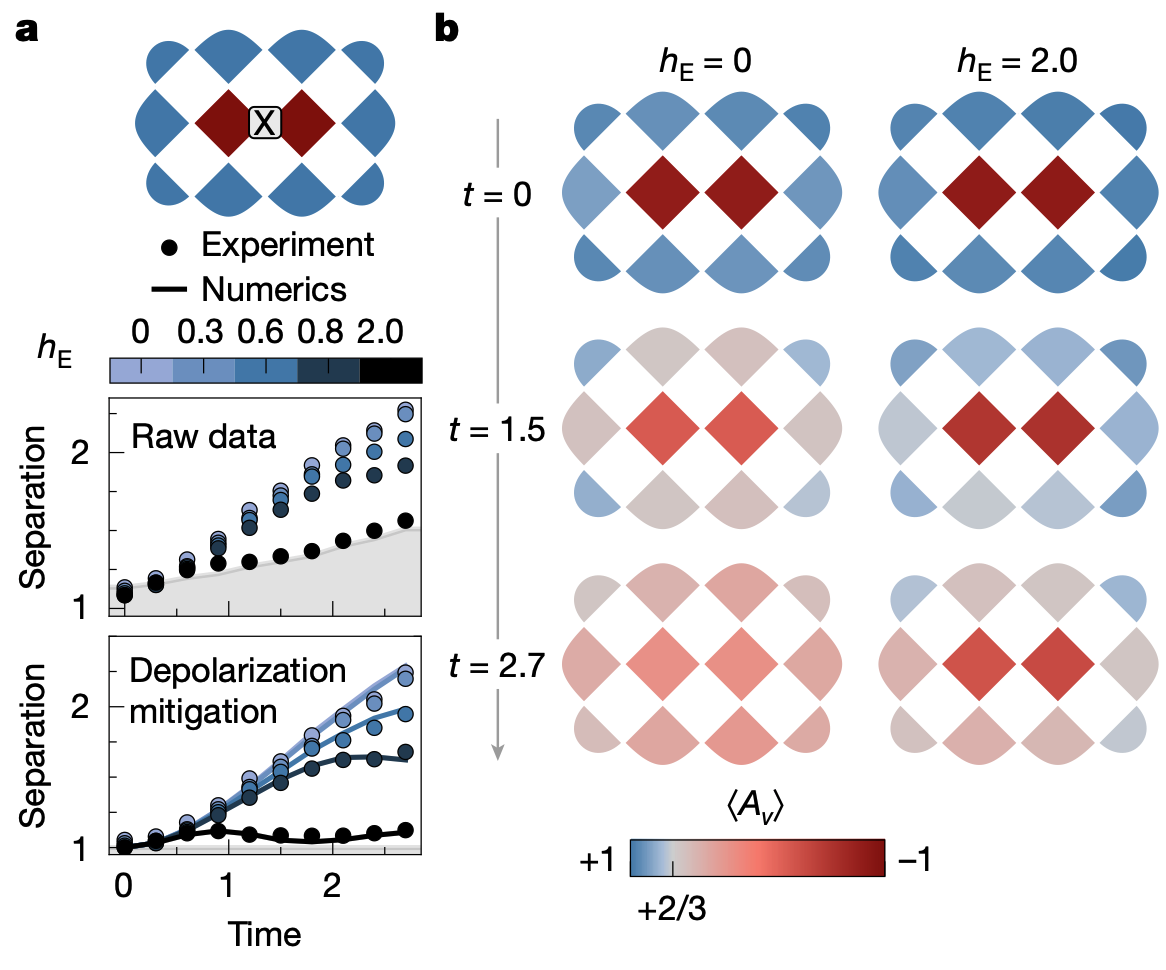
My research in this area takes several directions. I am have been fortunate to collaborate with Google Quantum AI and IBM (through Samsung) to perform experiments on their state-of-the-art quantum computers. This has allowed us to study various aspect of quantum state preparation, simulation of non-equilibrium dynamics, and the realisation of topological phases of matter on these devices. In addition to these experimental efforts, I am also interested in developing new algorithms and methods for simulating many-body quantum systems on quantum computers, particularly inspired by tensor network methods. I have also explored the possibilities of using current quantum computers for analogue simulations of time-dependent Hamiltonians by directly controlling the microwave pulses that manipulate superconducting qubits.
Topological Order
The conventional Landau paradigm classifies phases of matter through symmetry breaking and associated local order parameters. However, this framework fails to capture a broad class of phases known as topological phases, which are not characterized by local order but instead by non-local entanglement and global topological features. These phases exhibit exotic properties such as anyonic excitations and robust ground state degeneracy, making them of great interest for both fundamental physics and potential applications in quantum computing.
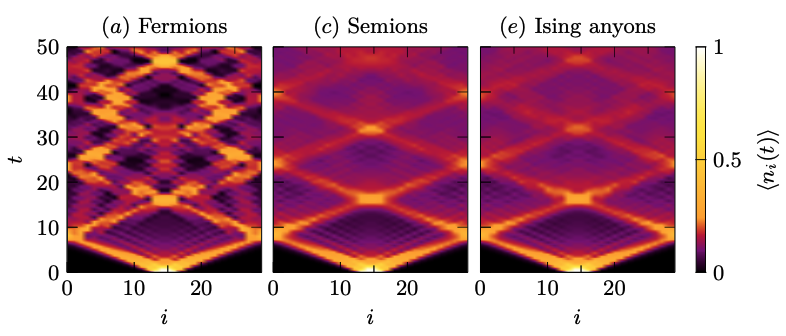
My research has recently focused on effective models of itinerant anyons, which are emergent quasiparticles in certain topological phatses that exhibit non-trivial braiding statistics. We have introduced tight-binding models for these anyons, and introduced numerical techniques to explore their phase diagrams and dynamics. I am also interested in how to use quantum computers to simulate and study topological phases of matter. My recent work has involved the realisation of the non-equilibrium topological order on a quantum processor.